Apuntes Sitemas inteligentes
El orden de precedencia en la lógica proposicional es –de mayor a menor prioridad–:
Por lo tanto, la oración: se puede escribir como:
BC = Base de conocimiento
Demuéstrese paso a paso, por aplicación de una secuencia de reglas de inferencia, que existe una contradicción en la siguiente base de conocimientos
{}
Solución:
- Tenemos la premisa (dada por la base de conocimientos).
- Tenemos la premisa (dada por la base de conocimientos).
- Tenemos la premisa (dada por la base de conocimientos).
Aplicamos la regla de Modus Ponens a las premisas 1 y 3, lo que nos da . Ahora tenemos una contradicción, ya que tenemos (de la premisa 4) y (de la premisa 2). Por lo tanto, la base de conocimientos es contradictoria.
Conviertre la siguiente oración en lógica de primer orden en cláusulas
donde K es una constante
Solución: Primero, eliminamos los implicadores (A implica B se convierte en no A o B):
Luego, movemos la negación hacia adentro (De Morgan’s Laws):
Después, eliminamos los cuantificadores existenciales:
Finalmente, convertimos a la forma normal de Skolem:
Donde f(x) y g(x) son funciones de Skolem que representan los valores específicos que y y z pueden tomar, respectivamente.
Describe formalmente en términos de un ejemplo en lógica proposicional el conceptro de consecuencia lógica e ilustralo también en terminos semánticos, mediante relaciones entre conjuntos
Solución:
La consecuencia lógica, denotada como , se refiere a la idea de que si es verdadero, entonces también debe ser verdadero. Es decir, sigue lógicamente de .
Por ejemplo, consideremos las proposiciones y . Aquí, podemos decir que porque si es verdadero (es decir, tanto como son verdaderos), entonces también debe ser verdadero.
En términos semánticos y de conjuntos, podemos pensar en y como conjuntos de mundos posibles o estados de cosas en los que estas proposiciones son verdaderas. Decir que es decir que el conjunto de mundos donde es verdadero es un subconjunto del conjunto de mundos donde es verdadero. En otras palabras, en todos los mundos donde es verdadero, también es verdadero.
Demustra formalmente, paso a pasao y muy claramente en lógica preposicional, que las siguientes expresiones
A.
Solución:
Para demostrar que , necesitamos mostrar que en todas las interpretaciones en las que es verdadero, también es verdadero.
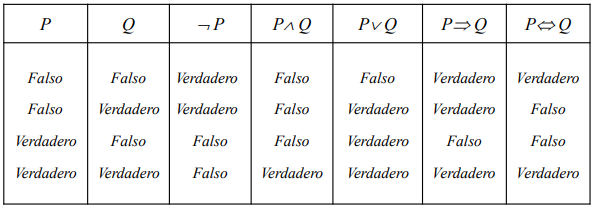
Podemos demostrar con una tabla de verdad. La tabla de verdad para estas expresiones es la siguiente:
| T | T | T | T | T | T | T |
| T | T | F | F | F | T | F |
| T | F | T | T | T | F | T |
| T | F | F | T | T | F | T |
| F | T | T | T | T | F | T |
| F | T | F | F | T | F | T |
| F | F | T | T | T | F | T |
| F | F | F | T | T | F | T |
Supongamos que es verdadero. Esto significa que si es verdadero, entonces también es verdadero.
Si es falso, entonces es verdadero (porque la implicación es verdadera si la primera parte es falsa), y también es verdadero (por la misma razón).
Si es verdadero, entonces es verdadero. Esto significa que si es verdadero, entonces es verdadero.
Si es falso, entonces es verdadero (por la misma razón que antes), y por lo tanto, también es verdadero (porque es falso).
Si es verdadero, entonces es verdadero. Esto significa que también es verdadero (porque la implicación es verdadera si la segunda parte es verdadera).
Por lo tanto, en todas las interpretaciones en las que es verdadero, también es verdadero. Por lo tanto, .
Como puedes ver, en todas las filas donde es verdadero, también es verdadero. Por lo tanto, .
B.
Solución:
Para demostrar que , necesitamos mostrar que en todas las interpretaciones en las que es verdadero, también es verdadero.
| T | T | T | T | F | F | F | T |
| T | F | F | F | F | T | F | F |
| F | T | F | F | T | F | F | F |
| F | F | T | F | T | T | T | T |
Supongamos que es verdadero. Esto significa que y tienen el mismo valor de verdad.
Si y son ambos verdaderos, entonces es verdadero y por lo tanto, es verdadero.
Si y son ambos falsos, entonces es verdadero y por lo tanto, es verdadero.
Por lo tanto, en todas las interpretaciones en las que es verdadero, también es verdadero. Por lo tanto, .
